432 & THE “FACTOR 9”
The Factor 9 concept is mentioned in the video called “Sonic Geometry: The Language of Frequency and Form” (by Eric Rankin and Alanna Luna). In this article we will take a closer look at the Factor 9 “formula”, it’s relationship to the Harmonic Series and the difference between the Factor 9 and “standard” temperamental implementation.
Official Website: www.sonicgeometry.com
SECOND VIDEO (2016)
FIRST VIDEO (2015)
NOTE: The number grid shown in the first video (12:52) contains some mistakes, more about this later.
FACTOR 9 AND THE HARMONIC SERIES OF D=9HZ
The “base frequency” or “Fundamental” of this grid is 9Hz. The other tones are the result of the implementation of the Harmonic Series. Depending on the Harmonic used as “starting point” of the a scale a different Musical Interval System is formed.
The number of tones in the scale formed from the Harmonic Series relates directly to the number of the Harmonic you start with. If you start from the 15th Harmonic, you would end up with a 15-Tone scale. This is not only the case when you use 9Hz as base frequency for this concept, this is simply the “nature” of the Harmonic Series.
For example:
12TH HARMONIC (TONIC A): 12-TONE SYSTEM
When we use A2=108Hz the first degree of the scale (12th-24th Harmonic of 9Hz) to it’s octave A3=216Hz, we would end up with a 12-Tone Temperament. On octave above 216Hz we find A4=432Hz.
14TH HARMONIC (TONIC C): 14-TONE SYSTEM
When we use C3=126Hz the first degree of the scale (14th-28th Harmonic of 9Hz) to it’s octave C4=252Hz, we would end up with a 14-Tone Temperament.
16TH HARMONIC (TONIC D): 16-TONE SYSTEM
When we use D3=144Hz as the first degree of the scale (16th-32nd Harmonic of 9Hz) to it’s octave D=288Hz, we would end up with a 16-Tone Temperament. D4=288Hz is a pretty familiar frequency for those who have been exploring 432-Tuning. We find the D4 at 288Hz with various 12-Tone Temperaments, such as the Pythagorean Temperament (in combination with Concert Pitch C4=256Hz or A4=432Hz) and Maria Renold’s “Scale of Fifths“. If you would like to use the 16-EDO system with Concert Pitch A4=432Hz, all frequencies (listed in the 3rd column) need to be pitched up with approximately 62 cents, the 16-EDO scale has “A4” at 416.8Hz, instead of 432Hz.
FACTOR 9 12T vs. 12-EDO vs. FIBONACCI-8 vs. RENOLD-I
The most “common” 12-tone scale belongs to 12-TET (12-Tone Equal Temperament) or 12-EDO (Equal Divisions of the Octave). I will try to “visualize” the difference between the “Factor 9 Temperament” and 12-TET in this article. If you do not know what a tuning system is made of, then please do read this article on my blog: Tuning Basics.
ABOUT 12-TET or 12-EDO
“12–EDO, perhaps better known as 12TET since it really is a temperament, is the predominating tuning system in the world today. It achieved that position because it is the smallest equal division which can seriously claim to represent 5-limit harmony, and because as 1/12 Pythagorean comma (approximately 1/11 syntonic comma) meantone, it represents meantone.
It divides the octave into twelve equal parts, each of exactly 100 cents each unless octave shrinking or stretching is employed. Its has a fifth which is quite good at two cents flat. It has a major third which is 13+2/3 cents sharp, which works well enough for some styles of music and is not really adequate for others, and a minor third which is flat by even more, 15+2/3 cents. It is probably not an accident that as tuning in European music became increasingly close to 12et, the style of the music changed so that the defects of 12et appeared less evident, though it should be borne in mind that in actual performance these are often reduced by the tuning adaptations of the performers.“
Source: Xenharmonic
Below a table with cents, ratios and more, comparing 12-EDO with FACTOR 9 12T, Fibonacci-8 and Renold-I, based on A=108Hz. I have transposed the complete scale in order to include 432Hz in the table so we start from A3=216Hz.
| Degree | Tone | 12-EDO | Factor 9 12T | Fibonacci-8 | Renold-I |
| 0 | A3 | 216 | 216 | 216 | 216 |
| 1 | A#/Bb | 228.8 | 234 | 230,4 | 229,1 |
| 2 | B | 242.5 | 252 | 240 or 243 | 243 |
| 3 | C | 256.9 | 270 | 259,2 | 256,4 |
| 4 | C#/Db | 272.1 | 288 | 270 | 273,4 |
| 5 | D | 288.3 | 306 | 288 | 257,7 |
| 6 | D#/Eb | 305.5 | 324 | 303,8 | 305,4 |
| 7 | E | 323.6 | 342 | 324 | 324 |
| 8 | F | 342.9 | 360 | 345,6 | 343,6 |
| 9 | F#/Gb | 363.3 | 378 | 360 | 364,5 |
| 10 | G | 384.9 | 396 | 384 or 388,8 | 386,5 |
| 11 | G#/Ab | 407.8 | 414 | 405 | 410 |
| 12 | A4 | 432 | 432 | 432 | 432 |
All frequencies above are rounded up to 1 digit behind the decimal point.
Below an example of a piece using the Factor 9 12-Tone scale (as listed above) by Derrick Scott van Heerden:
FACTOR 9 16-TONE By Derrick Scott van Heerden

“The factor 9 scale is really a harmonic scale, a one octave portion of the harmonic series repeated over octaves and played as a music scale on a multi-tonal instrument.
The long vertical column on the right (of the chart) shows the harmonic series for 9 Hz, while the bottom half shows the portion that makes the factor 9 scale repeated over 4 octaves to the right and left. There are a few missing notes in the factor 9 scale chart in the movie, here you can see that there are really 16 tones in each octave (16th to 31st harmonic).

Image on the right:
“This scale / slice of the harmonic series contains many intervals found in ‘pure’ versions of our 12 tone equal temperament scale and makes it seem obvious that our modern day 12 tone scale must have it’s roots in the harmonic series.“
More information at the source article: http://mathemagicalmusic.weebly.com/
DISADVANTAGES OF THE FACTOR 9 TEMPERAMENT
The most significant disadvantage of the Factor 9 Temperament is the specifications of some instruments, in particular acoustic instruments. Some acoustic instruments without temperamental issues are for example: the human voice, fret-less string instruments (like the Violin family), Trombone (a wind instrument without valves or tone-holes), the Harp and percussive instruments.
Naturally one could compose and produce music with modern Synthesizers, software with micro tuning capabilities or design / invent a new instrument based on this Temperament.
For instruments without micro-tonal tuning capabilities would be difficult to use the Factor 9 system, even in a 12-Tone scale.
NOTATION (SHEET MUSIC)
Up to a 14-tone scale the present notation system would work fine (adding a B#/Cb and E#/Fb to the scale). Notation of a 15-tone scale (or larger) using the traditional notation system can be a bit “tricky” and would require some time to study to be able to read it “prima vista“.
A 15-tone scale would look something like this (Easley Blackwood‘s notation system for 15 Equal Temperament):

A 24-tone scale would already require 3 variations in sharps and flats (24 Equal Temperament “Arab Tone System”):

SONIC GEOMETRY FIRST VIDEO: MISTAKES IN THE FACTOR 9 GRID
IMPORTANT FOOTNOTES ABOUT THE MOVIE “SONIC GEOMETRY:
Some numbers listed are simple miscalculations, but a more crucial mistake is that tones are missing in their grid!!! The scale/temperament displayed in the movie is a 13-tone system. But, after comparing the grid with the Harmonic Series we can conclude the grid shown in this video (12:52) is incorrect. Instead of a 13-tone system it would generate a 12 / 14 / 16-tone system if the implementation is done properly.
Also the “build-up” of the grid starts wrong, the “Factor 9” temperament is based on the tone D being 9Hz. If we set D as the first tone of the scale, then the first two frequencies listed in the 1st column belong to the “great octave” (stacking of 4.5Hz), while the rest of the tones listed in the first column belong to the “small octave” (above the “great octave”, stacking of 9Hz).
Movie screenshot: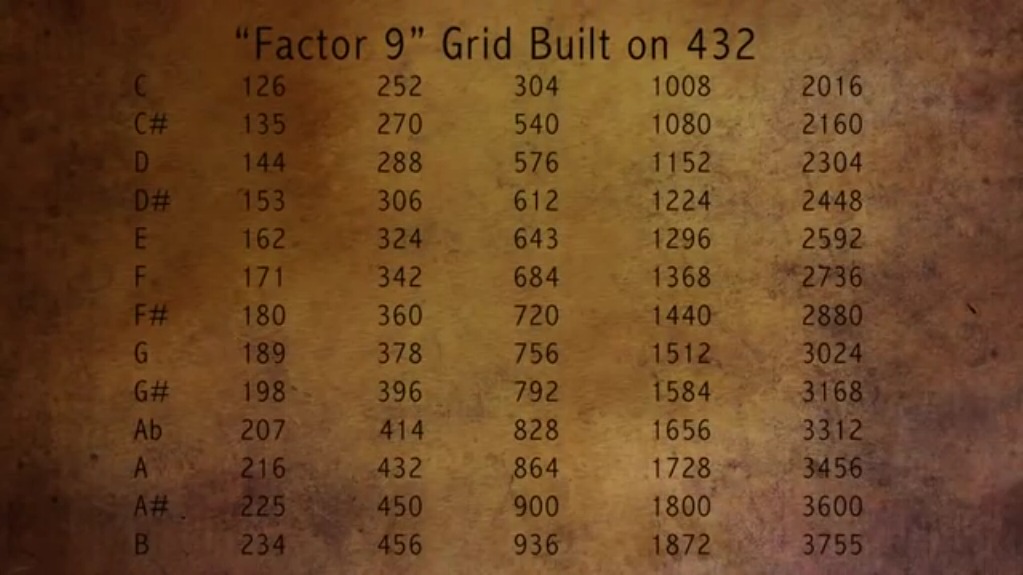
Missing frequencies:
- 130.5 (between C and C# in column 1) – “great octave” (stacking of 4.5Hz)
- 139.5 (between C# and D in column 1) – “great octave” (stacking of 4.5Hz)
- 243 (between 234 in column 1 and 525 in column 2) – “small octave ” (stacking of 9Hz)
- 486 (between 456 in column 1 and 504 – missing – column 3) – “1-line octave” (stacking of 18Hz)
- 504 & 522 (between 486 – missing – and 540 in column 3) – “1-line octave” (stacking of 18Hz)
- 972 (between 936 in column 3 and 1008 in column 4) – “2-line octave” (stacking of 36Hz)
- 1044 (between 1008 in column 4 and 1080 in column 4) – “2-line octave” (stacking of 36Hz)
- 1944 (between 1872 in column 4 and 2016 in column 5) – “3-line octave” (stacking of 72Hz)
- 2088 (between 2016 in column 5 and 2160 in column 5) – “3-line octave” (stacking of 72Hz)
Miscalculations:
B in column 2 has to be 468 instead of 456, 643 in column 3 has to be 648 and 3755 in column 5 has to be 3744.
Another footnote to make is related to what is being said in the movie about Concert Pitch and instruments. In the movie Eric Rankin mentions that most modern musical instruments have been tuned to 432 for decades (until A4=440Hz became the International Standard). This is not correct, 432Hz has never been a standard, and only some old instruments seem to / might have been build for (or close to) 432Hz as Concert Pitch such as 435Hz (Diapason Normal). There are many old instruments in museums, as well as old Pitchpipe (Church) organs with various pitches ranging between A4=360Hz up to A4=460Hz. Instruments for Baroque music (1600-1750) for example, were designed for a Concert Pitch 415Hz.
OTHER REFERENCES:
- www.sonicgeometry.com
- http://mathemagicalmusic.weebly.com/
- http://en.wikipedia.org/wiki/15_equal_temperament
- https://xenharmonic.wikispaces.com/15edo

